GPU-Accelerated Dimensionality Reduction with PCA & UMAP

Created on August 01, 2025

2025   ·   Visualization,   GPU

In fields ranging from computational biology to natural language processing, we are often confronted with high-dimensional data. Visualizing and making sense of datasets with thousands of dimensions and millions of samples is challenging. This is where dimensionality reduction techniques come into play. They allow us to compress data into a lower-dimensional space, making it suitable for both visualization and further analysis.

This guide will walk you through the classical two-step process for dimensionality reduction:

  1. Incremental Principal Component Analysis (PCA): A linear technique for initial dimensionality reduction with a constant memory cost.
  2. Uniform Manifold Approximation and Projection (UMAP): A non-linear method for uncovering intricate data structures.

The key to this workflow is the use of the NVIDIA RAPIDS cuML library to perform all computations on the GPU. For large datasets, this can reduce processing times from hours to minutes.

The Full Code is available at the end of this guide.

Author: Quentin Fournier (edited with LLMs)

Setting Up Your Environment

First, ensure you have the necessary libraries installed.

pip install scvi-tools pooch scanpy
pip install --extra-index-url=https://pypi.nvidia.com "cuml-cu12==25.6.*"

Next, import the necessary modules.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

# Dataset
import scvi
import scanpy as sc

# RAPIDS cuML for GPU-accelerated ML
from cuml import IncrementalPCA, UMAP

# Progress bar
from tqdm import tqdm

# For outlier filtering during visualization
from scipy.stats import zscore

# Display figures in higher quality
%config InlineBackend.figure_format='retina'

Loading a High-Dimensional Dataset

To demonstrate this workflow on a real-world example, we will use a single-cell RNA sequencing dataset of the human retina, easily accessible through scvi-tools. After loading, we perform standard preprocessing steps: filtering out cells and genes, normalizing the data, log-transforming it, and identifying the most highly variable genes to focus our analysis on. Our goal is to visualize the distinct cell types present in the tissue.

print("Loading and preprocessing the retina dataset...")
adata = scvi.data.retina()

# Basic filtering
sc.pp.filter_cells(adata, min_genes=100)
sc.pp.filter_genes(adata, min_cells=5)
sc.pp.normalize_total(adata, target_sum=1e4)
sc.pp.log1p(adata)
sc.pp.highly_variable_genes(adata)

# Extract the final data matrix and labels
adata_filtered = adata[:, adata.var.highly_variable]
embeddings = adata_filtered.X
labels = adata_filtered.obs['labels'].cat.codes.to_numpy()

print(f"Embeddings: {embeddings.shape}")

This will produce output similar to the following:

Loading and preprocessing the retina dataset...
Embeddings: (19829, 2830)

The Two-Step Dimensionality Reduction Process

This two-step reduction process starts with Principal Component Analysis (PCA). PCA is a computationally efficient technique that linearly projects data by identifying its most important features, preparing it for a subsequent, more complex non-linear mapping. Here, we’ll use the constant-memory IncrementalPCA, which processes large datasets in batches.

Tip: If your data is already at a manageable dimension (e.g., less than 2048), you can skip PCA.

print("\nPerforming Incremental PCA...")

# Define the number of dimensions and batch size for processing large data chunk by chunk.
n_components = 2048 # Adjust to explain ~90% of the variance.
batch_size = 8129 # Adjust based on the amount of GPU memory.

# Initialize the IncrementalPCA model from cuML
pca_model = IncrementalPCA(n_components=n_components, batch_size=batch_size)

# Process the data in batches to fit the PCA model incrementally.
for i in tqdm(range(int(np.ceil(len(embeddings) / batch_size))), desc="Processing Batches"):
    pca_model.partial_fit(embeddings[(i * batch_size) : ((i + 1) * batch_size)])

# Check how much of the original data's variance is captured by our components.
pca_embeddings = pca_model.transform(embeddings)
print(f"PCA Embeddings: {pca_embeddings.shape}")
print(f"Total variance explained: {pca_model.explained_variance_ratio_.sum():.2%}")

This will produce output similar to the following:

Performing Incremental PCA...
Processing Batches: 100%|██████████| 3/3 [00:04<00:00,  1.60s/it]
PCA Embeddings: (19829, 2048)
Total variance explained: 97.54%

We are now ready for the non-linear 2D projection. UMAP is a dimension reduction technique that can be used for visualization similarly to t-SNE, but also for general non-linear dimension reduction. We will utilize the GPU-accelerated UMAP implementation from RAPIDS cuML.

UMAP has two key hyperparameters:

  • n_neighbors: This is the most critical parameter. It balances local vs. global structure. Low values (5-15) focus on local detail, while high values (50-200) emphasize the global arrangement of clusters.

  • min_dist: This primarily controls the aesthetics of the final plot. Small values (0.0-0.1) create tight clusters, while larger values spread points out.

When using the fast build_algo="nn_descent" on GPU, you have access to several low-level parameters to fine-tune the trade-off between speed, GPU memory usage, and accuracy. These are especially useful for very large datasets:

  • nnd_n_clusters: Increasing this value (e.g., 4 → 8 → 16) partitions the search space into more pieces, which reduces peak GPU memory usage at a potential cost to performance.

  • nnd_graph_degree & nnd_intermediate_graph_degree: These control the connectivity of the nearest-neighbor graph during its construction. Set nnd_graph_degree to roughly 2 * n_neighbors (ideally a multiple of 32) and nnd_intermediate_graph_degree to 2 * nnd_graph_degree.

  • nnd_overlap_factor: A higher value generally improves accuracy at the cost of performance. The ratio of nnd_overlap_factor / nnd_n_clusters is a good indicator of the accuracy/performance trade-off.

  • You should avoid passing a random_state, as it forces cuML to fall back to a slower, exact algorithm (brute_force_knn).

# Initialize the UMAP model with parameters to control the projection.
umap_model = UMAP(
    n_neighbors=128, # Balances local vs. global structure.
    n_components=2, # Target dimension for visualization.
    min_dist=0.4, # Controls how tightly points are packed.
    n_epochs=1000, # Number of optimization iterations.
    build_algo="nn_descent", # Use the fast approximate nearest neighbor algorithm on the GPU.
    # Low-level keywords to fine-tune the nn_descent algorithm for performance and memory.
    build_kwds={
                "nnd_do_batch": True,
                "nnd_n_clusters": 32,
                "nnd_graph_degree": 256,
                "nnd_intermediate_graph_degree": 512,
                "nnd_overlap_factor": 8,
                },
)

# The `fit_transform` method performs the dimensionality reduction.
# `data_on_host=True` tells cuML the data is currently in CPU memory.
umap_projection = umap_model.fit_transform(pca_embeddings, data_on_host=True)

Visualizing the Results

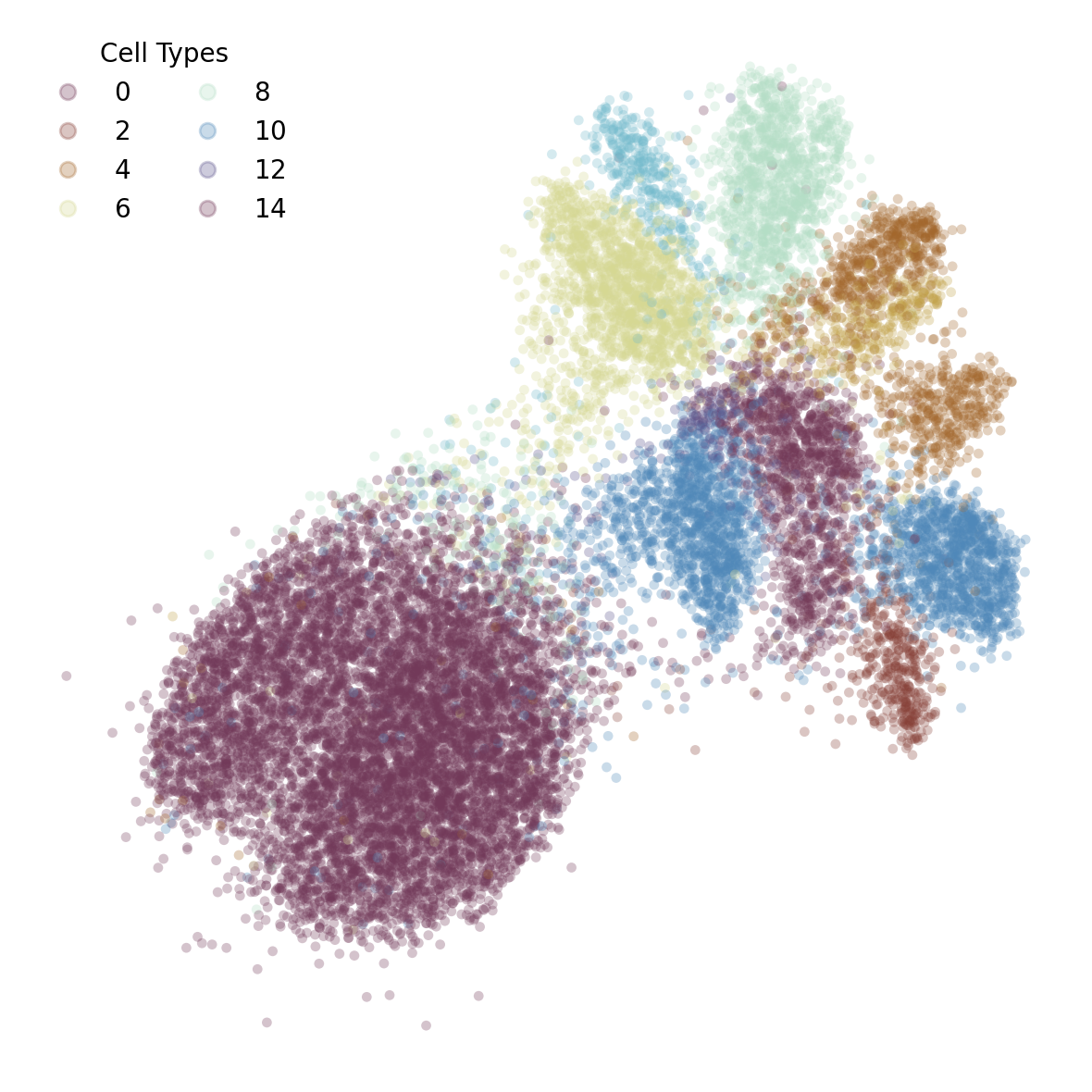
Now, we will create a scatter plot of our 2D projection. To improve clarity, we will filter out extreme outliers using a z-score. This effectively “zooms in” on the main distribution of the data.

# Filter extreme outliers for a clearer plot (central 95% of data)
z_scores = np.abs(zscore(umap_projection))
filter_mask = (z_scores < 1.96).all(axis=1)

# Create the scatter plot
fig, ax = plt.subplots(figsize=(6, 6))
romaO_cmap = ListedColormap(['#733957', '#874037', '#A3672C', '#C3A34B', '#D6D893', '#B4DEC6', '#74BBCD', '#4F88B9', '#5C538B', '#723959',])
scatter = ax.scatter(
    umap_projection[filter_mask, 0],
    umap_projection[filter_mask, 1],
    c=labels[filter_mask],
    s=15,
    alpha=0.3,
    cmap=romaO_cmap,
    edgecolors="none",
)
# Style the plot
legend = ax.legend(*scatter.legend_elements(), title="Cell Types", ncol=2, frameon=False)
ax.axis('off')
plt.tight_layout()
plt.show()

Despite some expected mixing, which reflects both the noisy nature of experimental data and true similarities between cell types, the final visualization reveals grouping of distinct cell types from the retina tissue.

Full Code

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

# Dataset
import scvi
import scanpy as sc

# RAPIDS cuML for GPU-accelerated ML
from cuml import IncrementalPCA, UMAP

# Progress bar
from tqdm import tqdm

# For outlier filtering during visualization
from scipy.stats import zscore

# Display figures in higher quality
%config InlineBackend.figure_format='retina'

# --- 1. Data Loading & Preprocessing ---
print("Loading and preprocessing the retina dataset...")
adata = scvi.data.retina()

# Basic filtering
sc.pp.filter_cells(adata, min_genes=100)
sc.pp.filter_genes(adata, min_cells=5)
sc.pp.normalize_total(adata, target_sum=1e4)
sc.pp.log1p(adata)
sc.pp.highly_variable_genes(adata)

# Extract the final data matrix, numeric labels for coloring, and string labels for the legend
adata_filtered = adata[:, adata.var.highly_variable]
embeddings = adata_filtered.X
labels = adata_filtered.obs['labels'].cat.codes.to_numpy()

print(f"Embeddings: {embeddings.shape}")

# --- 2. GPU-Accelerated PCA ---
print("\nPerforming Incremental PCA...")

# Define the number of dimensions and batch size for processing large data chunk by chunk.
n_components = 2048 # Adjust to explain ~90% of the variance.
batch_size = 8129 # Adjust based on the amount of GPU memory.

# Initialize the IncrementalPCA model from cuML, which is memory-efficient for large datasets.
pca_model = IncrementalPCA(n_components=n_components, batch_size=batch_size)

# Process the data in batches to fit the PCA model incrementally.
for i in tqdm(range(int(np.ceil(len(embeddings) / batch_size))), desc="Processing Batches"):
    pca_model.partial_fit(embeddings[(i * batch_size) : ((i + 1) * batch_size)])

# Check how much of the original data's variance is captured by our components.
pca_embeddings = pca_model.transform(embeddings)
print(f"PCA Embeddings: {pca_embeddings.shape}")
print(f"Total variance explained: {pca_model.explained_variance_ratio_.sum():.2%}")

# --- 3. GPU-Accelerated UMAP ---
# Initialize the UMAP model with parameters to control the projection.
umap_model = UMAP(
    n_neighbors=128, # Balances local vs. global structure.
    n_components=2, # Target dimension for visualization.
    min_dist=0.4, # Controls how tightly points are packed.
    n_epochs=1000, # Number of optimization iterations.
    build_algo="nn_descent", # Use the fast approximate nearest neighbor algorithm on the GPU.
    # Low-level keywords to fine-tune the nn_descent algorithm for performance and memory.
    build_kwds={
                "nnd_do_batch": True,
                "nnd_n_clusters": 32,
                "nnd_graph_degree": 256,
                "nnd_intermediate_graph_degree": 512,
                "nnd_overlap_factor": 8,
                },
)

# The `fit_transform` method performs the dimensionality reduction.
# `data_on_host=True` tells cuML the data is currently in CPU memory.
umap_projection = umap_model.fit_transform(pca_embeddings, data_on_host=True)


# --- 4. Visualization ---
# Filter extreme outliers for a clearer plot (central 95% of data)
z_scores = np.abs(zscore(umap_projection))
filter_mask = (z_scores < 1.96).all(axis=1)

# Create the scatter plot
fig, ax = plt.subplots(figsize=(6, 6))
romaO_cmap = ListedColormap(['#733957', '#874037', '#A3672C', '#C3A34B', '#D6D893', '#B4DEC6', '#74BBCD', '#4F88B9', '#5C538B', '#723959',])
scatter = ax.scatter(
    umap_projection[filter_mask, 0],
    umap_projection[filter_mask, 1],
    c=labels[filter_mask],
    s=15,
    alpha=0.3,
    cmap=romaO_cmap,
    edgecolors="none",
)
# Style the plot
legend = ax.legend(*scatter.legend_elements(), title="Cell Types", ncol=2, frameon=False)
ax.axis('off')
plt.tight_layout()
plt.show()


Enjoy Reading This Article?

Here are some more articles you might like to read next:

  • GPU-Accelerated XGBoost with Bayesian Hyperparameter Tuning
  • Beautiful Plots with Matplotlib